关键词:光伏电站 组件衰减 发电量估算 PVSYST模拟
1 前言
由于全球的能源危机问题,风能、太阳能等资源丰富的新能源逐渐占有重要的地位。世界太阳能光伏发电系统在近几年里保持持续高速增长,到2012年世界光伏发电累积装机容量已经达到102GW[1],并且成为增长速度最快的发电技术,光伏发电在20多个国家实现平价上网。
随着核心器件光伏组件的技术不断突破,效率不断提升,光伏发电系统的度电成本会逐渐的逼近传统的火力发电成本,同时随着储能技术的不断发展,届时,光伏发电系统由于它的系统规模随意、安装要求门槛低等优点将会在世界各地更普遍的应用开来。
在整个光伏系统应用市场里,目前并网光伏系统占有绝对主导的地位,皆依赖于并网光伏技术的不断发展成熟、相应设备性能成本的不断研发进步以及各国政府在政策方面的积极推进。
2 光伏发电系统的原理
由于光伏发电系统根据实际的应用大体上分为并网系统和独立系统[2],由于并网系统应用所占的份额较大,本文着重分析并网系统的发电量估算。
同时,由于系统规模和场合条件的不同,并网系统也有多种系统形式,本文对发电量的评估是按较大规模的光伏电站作为模型,且光伏电站所处的环境条件比较好。
图2-1为一个典型的大型地面电站的发电原理框图
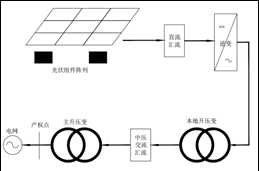
图2-1 大型电站发电原理简图
根据图示,通常在产权点会安装一个有效的电能计量表对光伏电站发电量进行计量,这是最为准确的统计数据。根据最初几年的计量统计数据对模拟数据进行分析修正,可以较为准确的预估今后的发电量。
3 光伏电站发电量损耗因素分析[3]
要在项目前期比较准确的预估光伏电站的发电量,除了对光伏电站的系统结构有深刻的了解外,也必须对主要的设备性能参数有很深刻的了解。同时,如果要对发电量进行更长年限的预估时,则必须全面考虑长时间内外界环境因素的影响和电站运营状况的预估。
分析第一年光伏电站的发电量估算时,通常需要考虑的损耗因素如下:
⑴倾斜面太阳光辐照量修正;
⑵组件表面灰尘等异物挡光的影响;
⑶温度对光伏组件输出的影响;
⑷光伏组件的自身衰减;
⑸组串内组件的匹配损失;
⑹方阵前后排之间的阴影遮挡损失;
⑺直流线路损失;
⑻逆变器转换效率损失;
⑼本地变压器损耗;
⑽交流线路损失;
⑾主变压器损耗;
⑿电站自用电损耗;
⒀停机时间损失;
通常采用PVSYST软件模拟发电量时,没有考虑自用电和停机时间的损耗,只是考虑其它因素的一个综合数据。
分析后面24年的光伏电站发电量时,运营管理是最主要的影响因素,但预估性差,通常假定其与其它因素不发生变化,只是考虑光伏组件自身的衰减。
4 光伏组件功率的衰减分析
在实际中,光伏组件在制造出来后就一直处于衰减的状态,不过在包装内未见光时衰减非常慢,一旦开始接受太阳光照射后,衰减会急剧加快,衰减一定比例后逐渐稳定下来,如图4-1所示的第一年衰减曲线模型示意图,
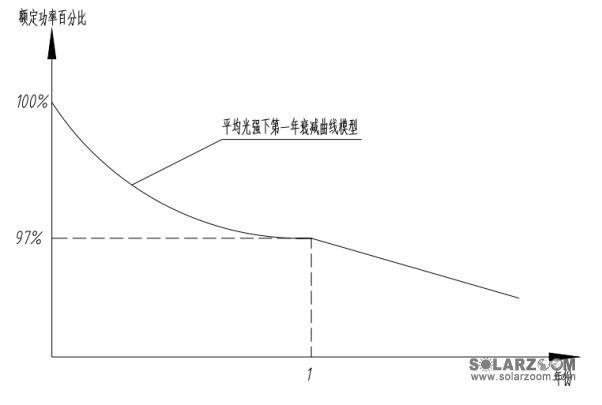
图4-1 光伏组件第一年衰减曲线模型
图4-1中第一年3%的总衰减数据取自正泰太阳能多晶硅组件的25年衰减保证当中,其25年衰减保证如图4-2所示,
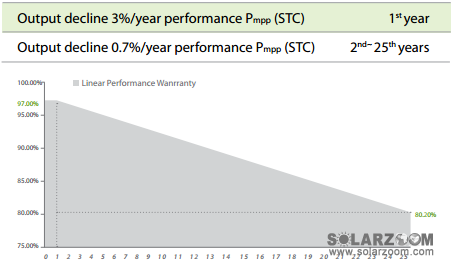
图4-2 光伏组件衰减曲线
由于初始阶段的衰减与光强有着直接的关系,因此在第一年内,在平均光强条件下,基本上前期呈现急剧衰减,后期逐渐平稳的状态。但是实际上,一个光伏电站从组件开始安装到最后开始并网发电这个时间跨度都是不一定的,到开始计量发电量的时候,组件可能已经进行了一定比例的衰减了,为了减小实际情况与理论估算的误差,除了在质保起始时间做要求外,一般组件在出厂时都会有一定比例的正功率偏差,这个正功率偏差可以覆盖一部分由于一些人为因素导致的组件在没有发电的情况下的一些衰减损耗。
所以在理论计算上,发电量模拟计算的额定功率起始点可以等同于光伏组件出厂时的额定功率,而且一年内组件的衰减可视为线性衰减。
5 光伏电站发电量的估算
光伏电站年发电量计算事实上是光伏电站实时输出功率与时间的函数积分,如图5-1所示,
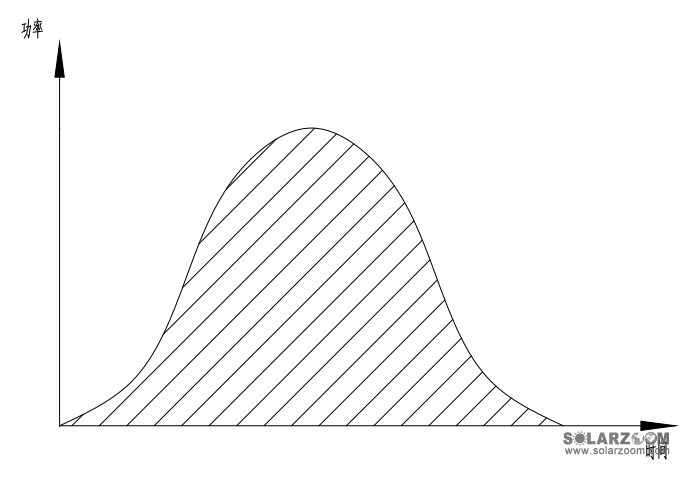
为了便于计算,通常将上图等效为标准光强下的输出功率与峰值日照小时数的矩形图,如图5-2所示,
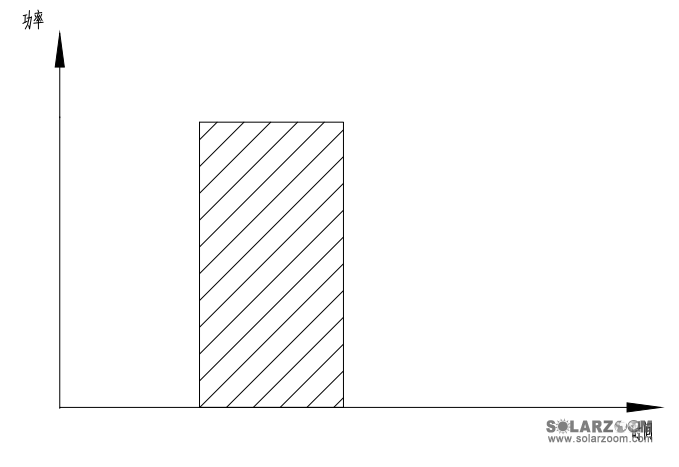
图5-2 光伏发电功率-时间等效矩形图
等效功率P´=额定装机功率P×系统综合效率η(式5-1)
为便于计算光伏电站25年的发电量,可将式5-1表述为式5-2,如下
等效功率P´=额定装机功率P×组件平均效率η1×系统其它损失因素综合效率η2(式5-2)
综合上述,光伏电站年发电量Q=额定装机功率P×组件平均效率η1×系统其它损失因素综合效率η2×峰值日照时间H×365天,在25年期限中,除了组件平均效率η1,其它项的乘积可视为一个不变的常数Q?,则最终的表达式为光伏电站年发电量Q= Q×组件平均效率η1(式5-3)。
组件平均效率η1——(年初组件额定容量比例+年末组件额定容量比例)/2
比例的正功率偏差,这个正功率偏差可以覆盖一部分由于一些人为因素导致的组件在没有发电的情况下的一些衰减损耗。
所以在理论计算上,发电量模拟计算的额定功率起始点可以等同于光伏组件出厂时的额定功率,而且一年内组件的衰减可视为线性衰减。
综上所述,以正泰太阳能多晶硅组件的衰减保证为例,25年的年组件平均效率如下表所示:
|
年份 |
年初组件容量比例 |
年末组件容量比例 |
年组件平均效率 |
|
1 |
100.00% |
97.00% |
98.50% |
|
2 |
97.00% |
96.30% |
96.65% |
|
3 |
96.30% |
95.60% |
95.95% |
|
4 |
95.60% |
94.90% |
95.25% |
|
5 |
94.90% |
94.20% |
94.55% |
|
6 |
94.20% |
93.50% |
93.85% |
|
7 |
93.50% |
92.80% |
93.15% |
|
8 |
92.80% |
92.10% |
92.45% |
|
9 |
92.10% |
91.40% |
91.75% |
|
10 |
91.40% |
90.70% |
91.05% |
|
11 |
90.70% |
90.00% |
90.35% |
|
12 |
90.00% |
89.30% |
89.65% |
|
13 |
89.30% |
88.60% |
88.95% |
|
14 |
88.60% |
87.90% |
88.25% |
|
15 |
87.90% |
87.20% |
87.55% |
|
16 |
87.20% |
86.50% |
86.85% |
|
17 |
86.50% |
85.80% |
86.15% |
|
18 |
85.80% |
85.10% |
85.45% |
|
19 |
85.10% |
84.40% |
84.75% |
|
20 |
84.40% |
83.70% |
84.05% |
|
21 |
83.70% |
83.00% |
83.35% |
|
22 |
83.00% |
82.30% |
82.65% |
|
23 |
82.30% |
81.60% |
81.95% |
|
24 |
81.60% |
80.90% |
81.25% |
|
25 |
80.90% |
80.20% |
80.55% |
表5-1 25年组件额定容量变化预测表
|
年份 |
年发电量 |
年份 |
年发电量 |
|
1 |
Q1=Q´×98.5% |
14 |
Q1×(88.25%/98.5%) |
|
2 |
Q1×(96.65%/98.5%) |
15 |
Q1×(87.55%/98.5%) |
|
3 |
Q1×(95.95%/98.5%) |
16 |
Q1×(86.85%/98.5%) |
|
4 |
Q1×(95.25%/98.5%) |
17 |
Q1×(86.15%/98.5%) |
|
5 |
Q1×(94.55%/98.5%) |
18 |
Q1×(85.45%/98.5%) |
|
责任编辑:carol 碳索光伏网版权声明: 本站标注"来源:碳索光伏网"或"索比咨询"的作品,均属www.solarbe.com合法享有版权或已获授权的内容。未经书面许可,任何单位或个人不得以转载、复制、传播等方式使用。 经授权使用者,须严格在授权范围内使用,并在显著位置标注来源,不得修改内容。违规者将依据《著作权法》追究法律责任,本站保留进一步追偿权利。 推荐新闻
|

